1. Zweck und Zielsetzung
1.1 Allgemein
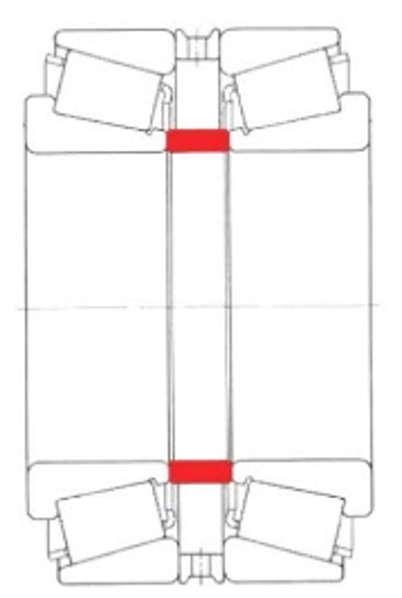
Bild 1
In der Praxis existieren mehrere Methoden, Kegelrollenlager zu paaren und vorzuspannen: Back-to-Back (O-Anordnung), Face-to-Face (X-Anordnung), Tandem (zur Erhöhung der axialen Tragfähigkeit) sowie mit Spiel gepaart, starr vorgespannt oder federgespannt. Bei werksseitig gepaarten Sätzen (Duplex-Sätze) sind Vorspannung bzw. Axialspiel durch beiliegende Abstandsringe vordefiniert.
Das Paaren nicht werksseitig abgestimmter Lager erfordert hingegen zusätzlichen Aufwand: Vorab-Vermessung relevanter axialer Ist-Abmessungen der Lager und Gehäuse, Festlegung der Zielwerte für das Axialspiel – und bei der O-Anordnung – neben einem äusseren Distanzringes, auch die Fertigung eines inneren, mit ausreichender Genauigkeit geschliffenen Einstellrings (Bild 1), gemäss den Anforderungen aus den Einsatzbedingungen.
1.2 Vorspannprinzip
Soll nun ein spezifisch vorgespanntes Kegelrollen-Lagerpaar in fester O-Anstellung über das Gehäuse abgestützt werden, muss zu Errechnung der effektiven Spacer-Länge auch die Gehäuseweite (GW) erfasst werden (Bild 2). Die Darstellung berücksichtigt die geometrischen Soll-Abstände und keinerlei physikalischen Effekte wie Ausdehnung oder Passung.
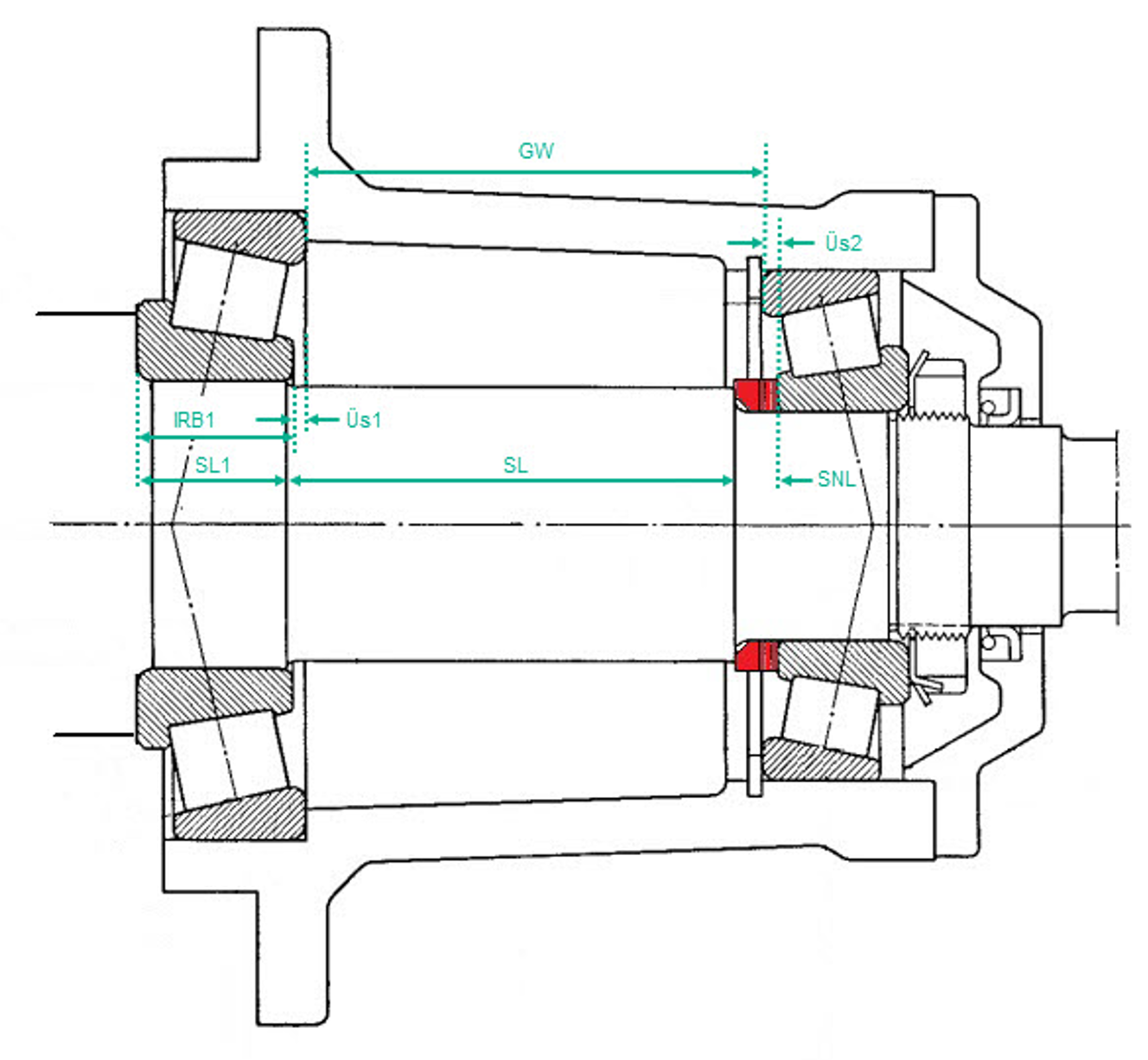
Bild 2
Die gemessenen stirnseitigen Überstände (Bild 3) dienen in Summe mit der Gehäuseweite der Ermittlung des inneren axialen Abstandes zwischen den beiden Lager.
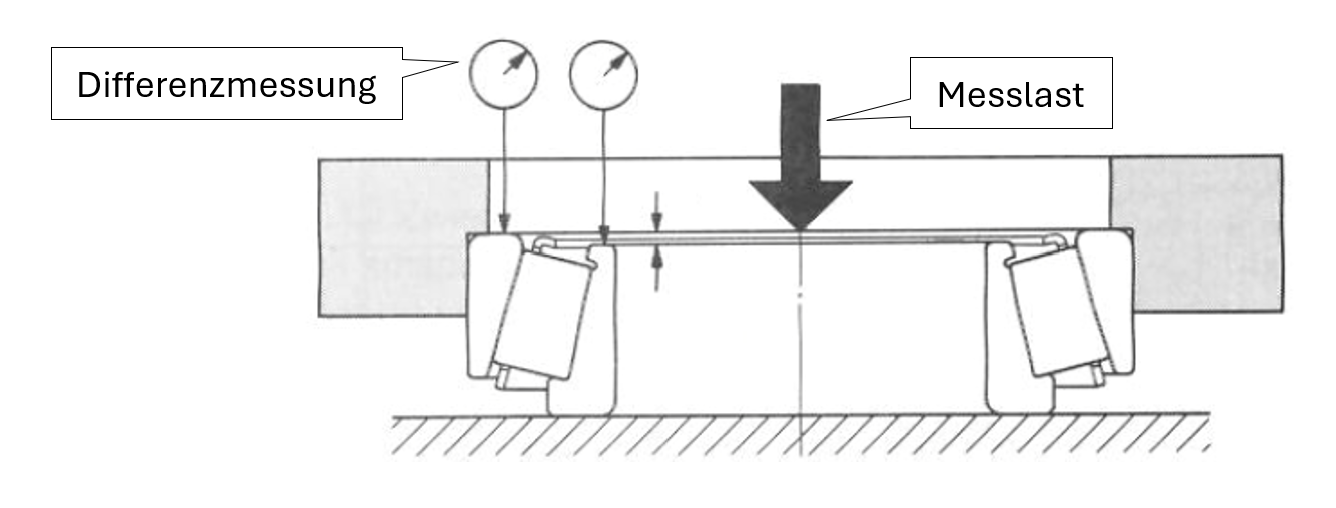
Bild 3
Damit lässt sich auch die Spacer-Nennlänge (SNL) ermitteln, durch: SNL = (GW) + Überstande (Üs1 & 2) + Innenring-Breite Lager 1 (IRB1) – Wellensegmente (SL1 & SL):
SNL = GW + Üs1 + Üs2 + IRB – (SL1+ SL)
Die zu definierende axiale Kürzung des Spacers entspricht nach dynamischem, thermischem und physikalischem Einfluss dem Vorspannweg des Kegelrollenlager-Paars. Diese Einflüsse lassen sich rechnerisch und zeitsparend mit MESYS ermitteln.
1.3 Anwendungs-Beispiel
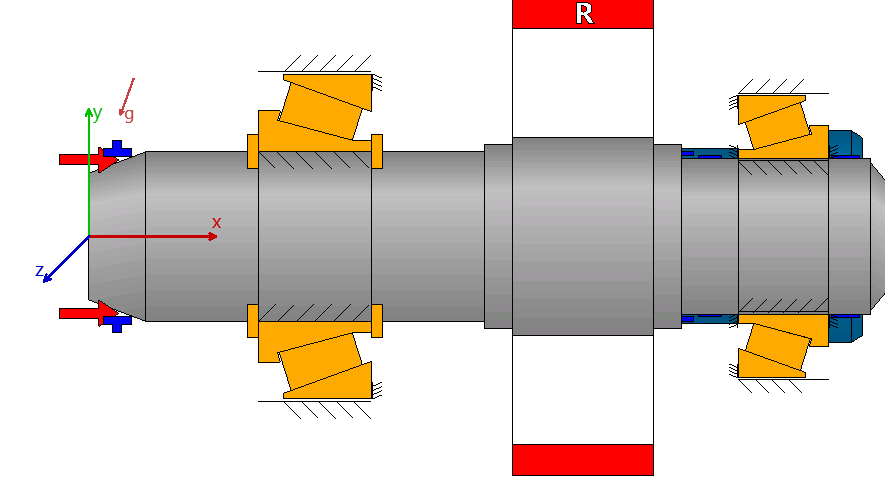
Bild 4
Vorliegendes Dokument erläutert die Auslegung eines fest vorgespannten Kegelrollen-Lagerpaares in O-Anordnung, zur Abstützung einer Getriebeausgangswelle in einer Marineanwendung. Ziel ist es, mithilfe der MESYS-Wellenberechnung direkt die erforderliche Lagervorspannung unter Berücksichtigung aller messbaren Einflüsse aus einem definierten Betriebszustand zu bestimmen. Eine geeignete Lagervorspannung wird durch Definition des Vorspannwegs festgelegt.
Diese wird einerseits mittels Distanzhülse und andererseits der durch die Wellenmutter erzeugten und notwendigen Klemmkraft erreicht.
1.4 Rahmen & Besonderheiten der Anwendung
Die wahrscheinlichsten Lastfälle wie Propellerschub vorwärts (ahead) und rückwärts (astern) werden betrachtet. Die resultierenden Zahnradkräfte einer schrägverzahnten Stufe fliessen als Tangential-, Radial- und Axialkomponenten in die Belastungswirkung ein.

Bild 5
Umgebungsbedingungen: Öl-Schmierung, Temperaturdifferenzen Welle/Gehäuse, Montage- und Passungsinterferenzen (IR/OR) werden berücksichtigt.
Aufgrund des zeitlich überwiegenden Vorwärtsschubs kommen ungleiche Lagerdimensionen zum Einsatz.
1.5 Zielumsetzung und Nachweisstrategie
Die Auslegung soll, soweit dies andere Randbedingungen nicht tangiert, in jedem Zustand eine Lager-Mindestlast aufweisen. Schlupfzustände – insbesondere bei starken Lastwechseln – und das daraus resultierende Abheben (Lift-off) der Rollen soll ausgeschlossen werden. Die damit einhergehende höhere Temperaturentwicklung infolge entsprechend erhöhter Grundlast aus Vorspannung ist bei Ölschmierung vertretbar.
Die Lebensdauer wird über ein transparentes Lastkollektiv nachgewiesen. Dazu werden die vier Betriebszustände STOP, IDLE, AHEAD und ASTERN jeweils mit einer festen Übersetzung betrachtet, mit hypothetischen Zeitanteilen gewichtet und zu einer äquivalenten Lagerbelastung verdichtet. Auf dieser Basis wird ein Revisionsintervall von 7 Jahren oder eine modifizierte Referenz-Lebensdauer von mindestens 11’200 h überprüft.
Die korrekte Anstellkraft der Mutter ist aus den beitragenden Kräften abzuleiten. Ausgangspunkt ist die Kraft, die für Verschiebung der Ringe unter Interferenz zur Welle oder Gehäuse erforderlich ist. Dazu kommt die resultierende Vorspannkraft im Lagerpaar. Schliesslich ist eine zusätzliche Klemmkraft der Mutter zu berücksichtigen, welche Veränderungen aus dynamischen Belastungen auf das Montagepaket kompensieren soll. Aus der Summe der Kraftanteile ergibt sich die einzustellende Anstellkraft bzw. das hier nicht weiter verfolgte zugehörige Mutter-Anzugsdrehmoment.
Die Robustheit der Vorspannungsauslegung ist durch Parametrierung der Passungs-Toleranzlagen und aus Annahme von daraus entstehenden Temperaturgefällen, unter einer mit Bezug zu System-Lebensdauer dem Lastkollektiv entsprechenden singulären äquivalenten Belastung darzustellen.
2. Ausgangslage
2.1 Antriebskonzept
Die untersuchte, hypothetische Anwendung ist die Getriebeausgangswelle eines Marine-Getriebes. Für den Vorwärtsschub von 25 kN (ahead) wird ein anliegendes Drehmoment von 2500 Nm zugrunde gelegt, für den Rückwärtsschub (astern) 1500 Nm – jeweils bei konstanter Drehzahl von 1600 rpm.
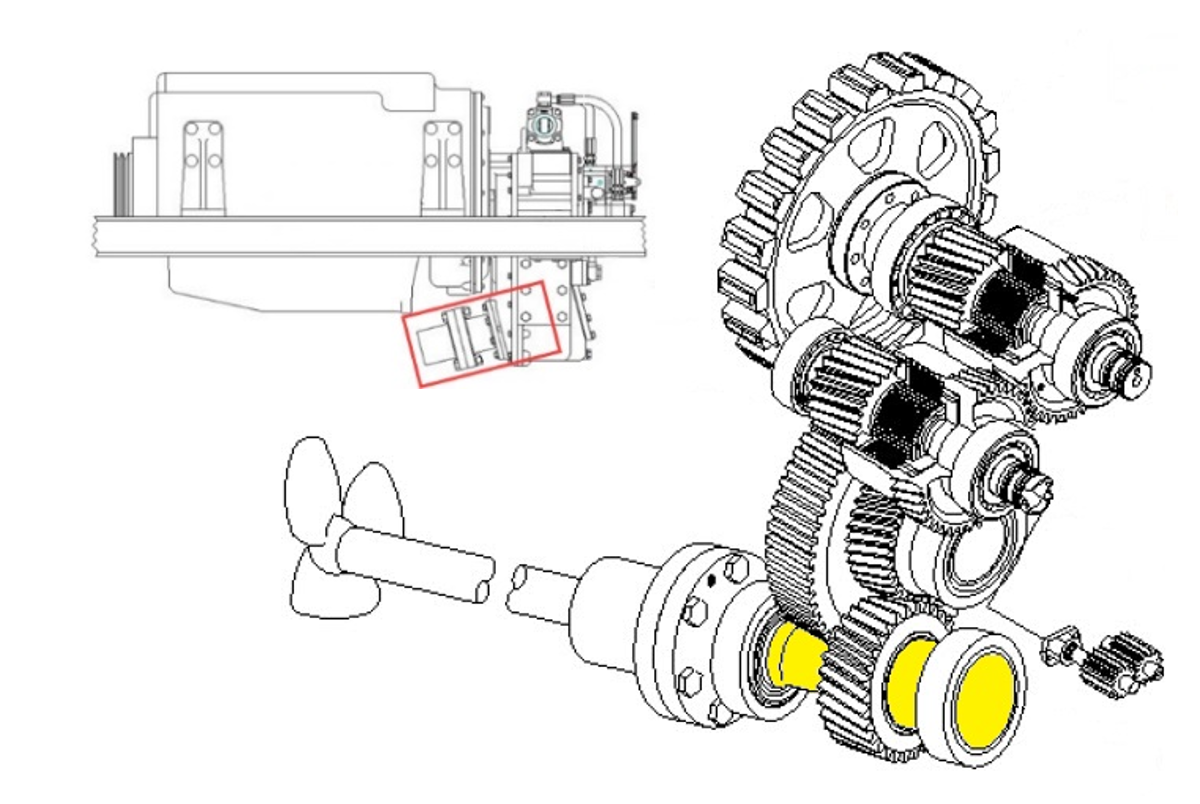
Bild 6
Die zugehörigen Schubkräfte werden ohne Detailauslegung des Propellers über den Open-Water-Formalansatz hergeleitet. Dafür werden die dimensionslosen Propellerkennzahlen KT (Thrust) und KQ (Torque) verwendet.
Tprop = KT/KQ * Q/D
Bei fixem Propellerdurchmesser D und konstantem Quotienten KT/KQ am betrachteten Betriebspunkt ist der Schub proportional zum Schaftmoment Q. Damit lassen sich die Schubniveaus aus den Drehmomenten konsistent ableiten.
2.2 Stirnrad
Zur Kraftübertragung ist ein Stirnrad mit Schrägungswinkel von 20° und weiteren, in Bild 7 einsehbaren Charakteristiken im Einsatz:
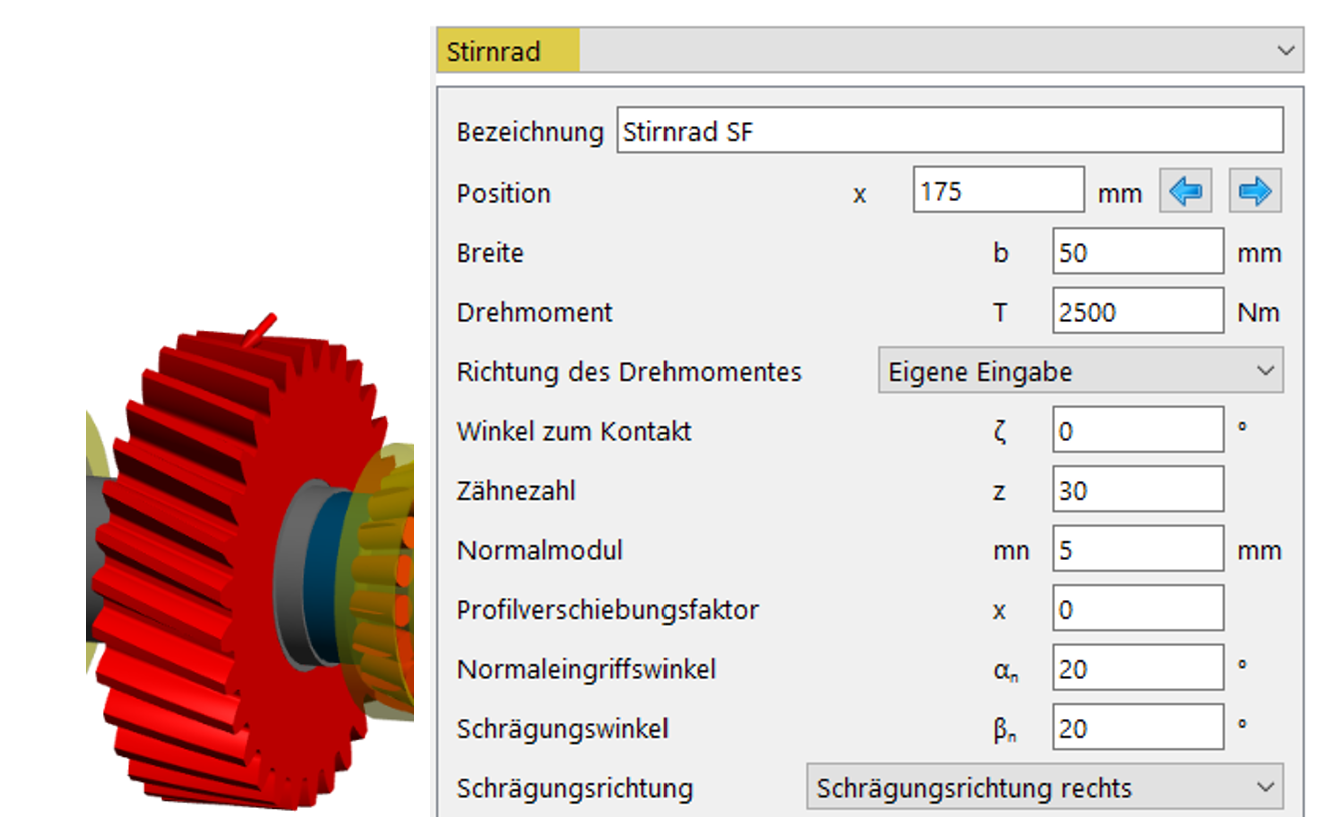
Bild 7
2.3 Lagerungskonzept
Die Vollwelle mit aufgesetztem Zahnrad ist über zwei Kegelrollenlager in fest verspannter O-Anordnung gelagert. Zum Einsatz kommen folgende Verzahnungs- und Lagerkonfigurationen:
– Zahnrad mit b = 50 mm; z = 30; mn = 5; Schrägungswinkel βn = 20°
– Outboard: 60 x 115 x 40 mit 20° Druckwinkel; C = 156.064 kN, C0 = 211.631 kN
– Inboard: 55 x 100 x 32 mit 19.8° Druckwinkel; C = 111.023 kN, C0 = 147.668 kN
Die O-Anordnung bietet hohe Kippsteifigkeit und eine eindeutige Abstützung der Axialkräfte in beide Richtungen; das grössere Lager mit 20° Druckwinkel Outboard adressiert den dominanten Ahead-Schub. Die feste Vorspannung lässt sich über einen definierten Vorspannweg (Spacer + Mutternklemmkraft) unter Berücksichtigung von Passungen und Temperaturdifferenzen vorab berechenbar einstellen.
3. Einstellgrössen
3.1 Mindestbelastung
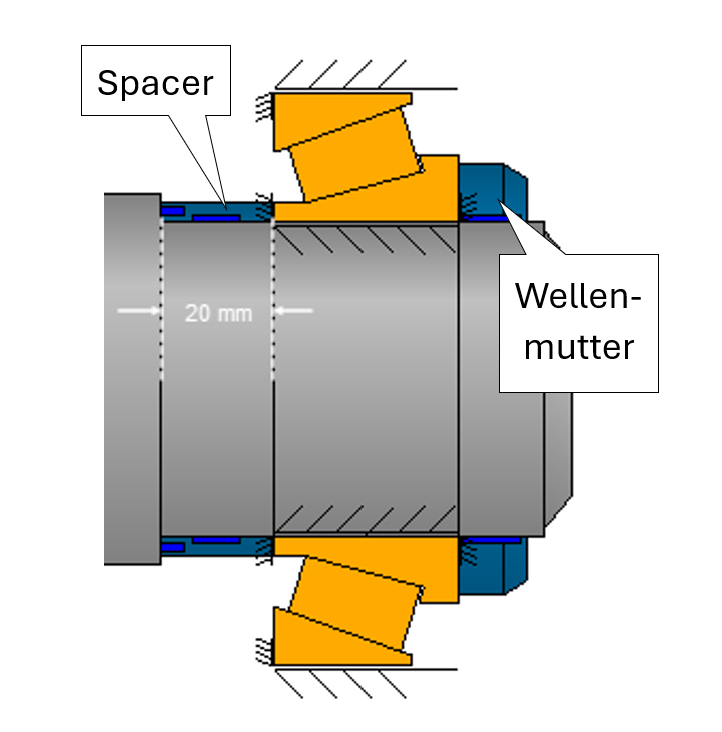
Bild 8
Der Vorspannweg wird mittels Variation der Spacer-Länge mit Nennmass 20 mm (Bild 8) durch Parametervariation so gewählt, dass die minimale Rollenpressung (pmin) auch in kritischem Lastkollektiv-Element soweit dies möglich ist deutlich über Null bleibt.
3.2 Lebensdauer
Ein Kompromiss zwischen Mindestlast und Lebensdauer, welche in Zusammenhang mit der durch Vorspannung entstehender Verlustleistung steht, soll gefunden werden.
3.3 Wellenmutter-Spannkraft
Die Mutter-Spannkraft wird aus der Summe der Kraftanteile an die notwendige Gesamt-Spannung, wie Lager-Verschiebekraft (Montagekraft), Lager-Vorspannkraft und zusätzliche Festhaltekraft bestimmt und so eingestellt, dass sie die Zielvorspannung des Lagerpaketes einhalten kann.
3.4 Toleranzfelder
Schliesslich wird auf Basis der Resultate einer Parametervariation das Verhalten in den Kombinationen der Toleranzfelder für Passungen und entsprechenden Temperaturgefällen eine Bestätigung für die gewählte Einstellung gesucht.
4. Methodik zur Bestimmung der Zielwerte
4.1 Elastische Ring-Aufweitung
Unter axialer Vorspannung kann bei Spielpassungen ein Aussenring unter der Wirkung des Druckwinkels radial aufweiten der Innenring schrumpfen. Beides reduziert die wirksame Vorspannung im Betrieb. Diese Effekte werden zusammen mit Passungen und Temperaturdifferenzen in der Berechnung berücksichtigt, damit der eingestellte Vorspannweg im Betrieb den Zielwert trifft. Die Berücksichtigung der elastischen Aufweitung für die Ringe ist daher für beide Lager aktiviert.
4.2. Erweitertes Berechnungsmodell
Outboard, B1:
Das ‚erweiterte Berechnungsmodell‘ (Bild 9) erlaubt es, Elemente für axiale und radiale Kontakte zu definieren. Es ermöglicht auch die Berücksichtigung von Axial- Spiel zwischen Lagerring und Welle oder Gehäuse.
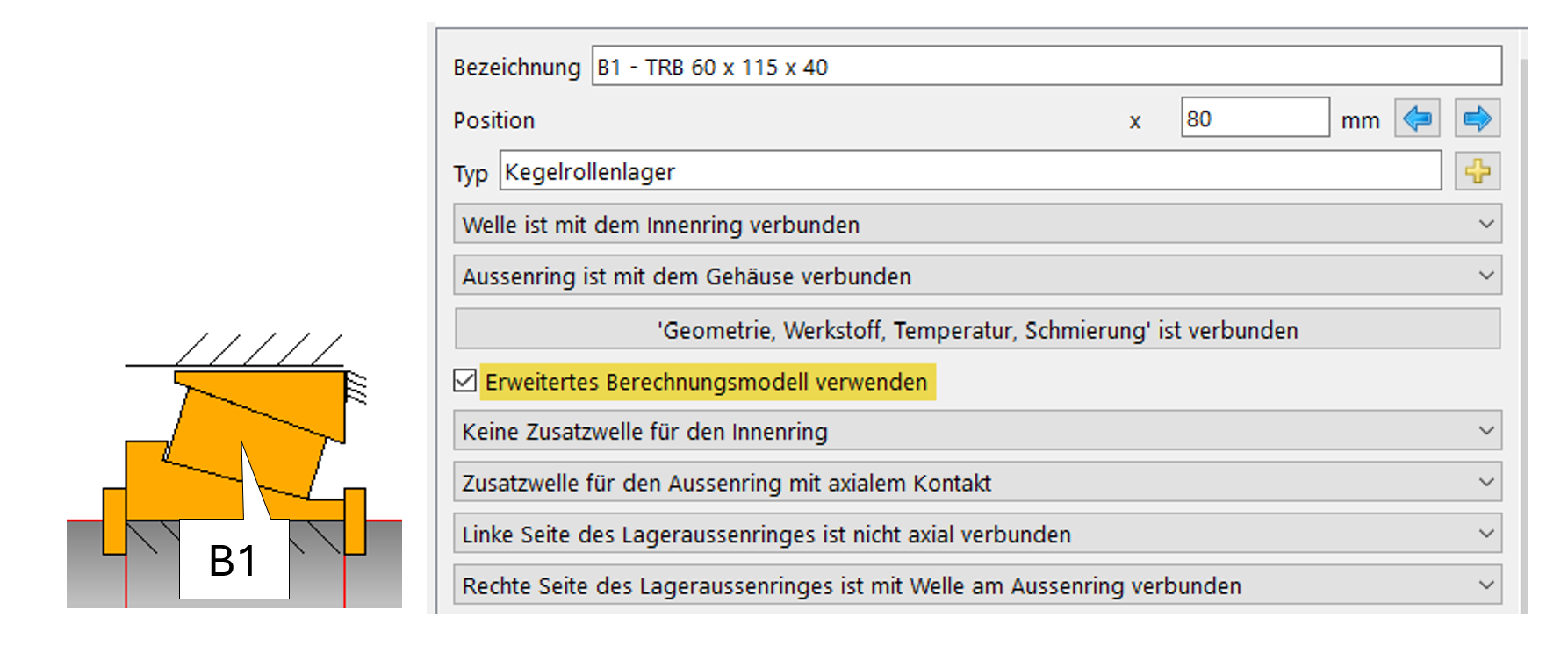
Bild 9
Inboard, B2:
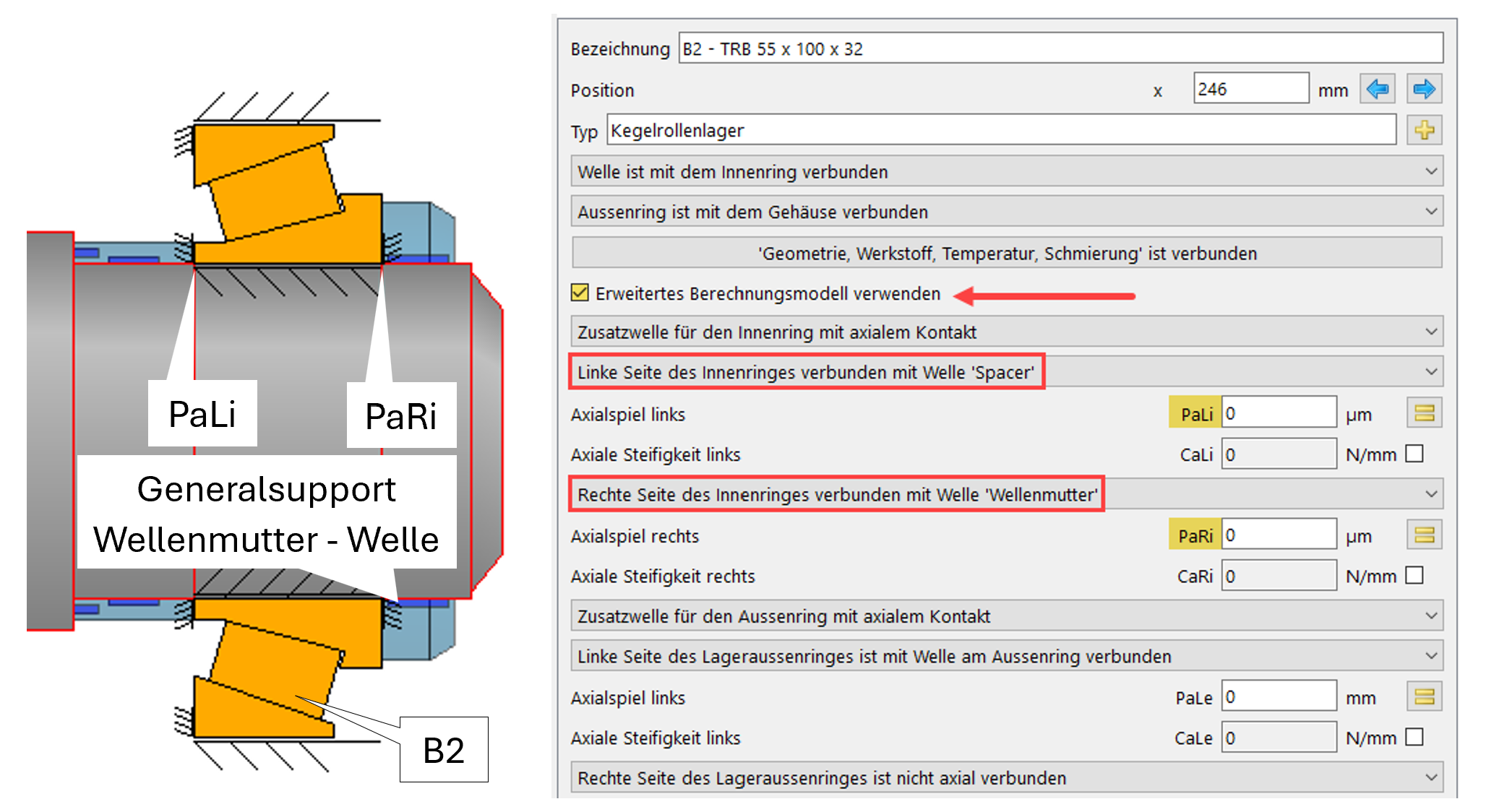
Bild 10
4.3 Lastkollektiv
Ein hypothetisches Lastkollektiv gemäss Tabelle 1 ist aktiviert:
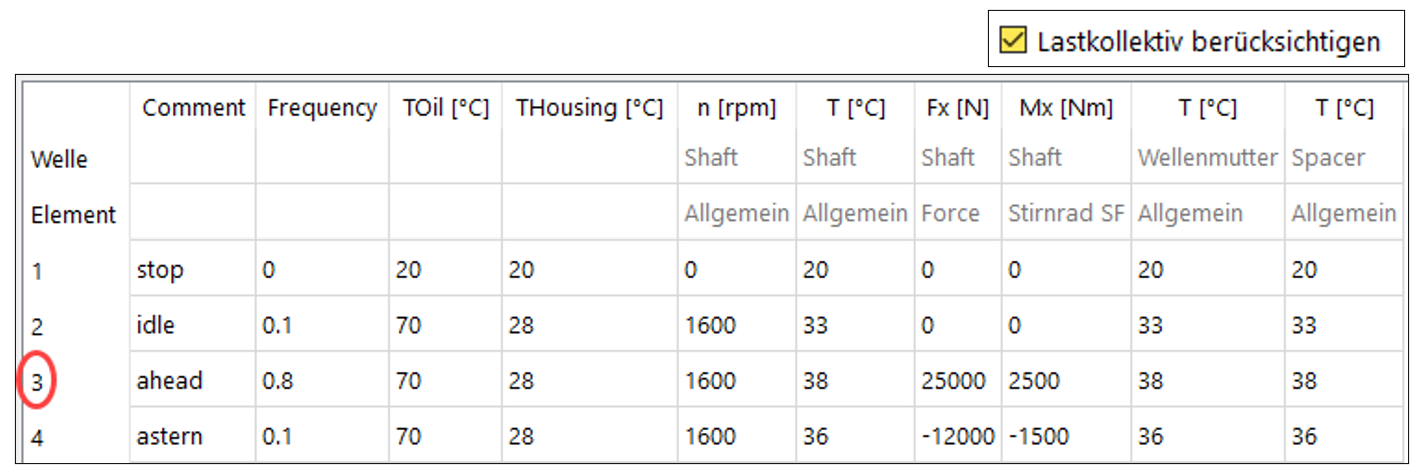
Tabelle 1
Element 3 ist mit Bezug auf Lagerbelastung, Verkippung und Schlupf als kritischer und somit interessierter Zustand zu bezeichnen (Tabelle 1).
4.4 Passungen
4.4.1 Generell

Bild 11
Präzisionsklasse, Passungen, Rauheiten und Gehäusedurchmesser gemäss Bild 11 sind berücksichtigt. Diese im Toleranzreport ausgegebenen Einstellungen erzeugen für B2 unter Lastspektrum-Element 1 die Montagekräfte gemäss 4.6.2.
4.4.2 Passungs-Toleranzlagen
Eine preliminäre Untersuchungen zu idealem Vorspannweg ist praktischerweise unter einer Toleranzlage ‚mittleren Spiels‘ abzuwickeln. In einem nachfolgenden Schritt sollen aber zur ev. Absicherung gegenüber allen Bedingungen, auch Untersuchungen abweichend des Mittelwertes erfolgen.
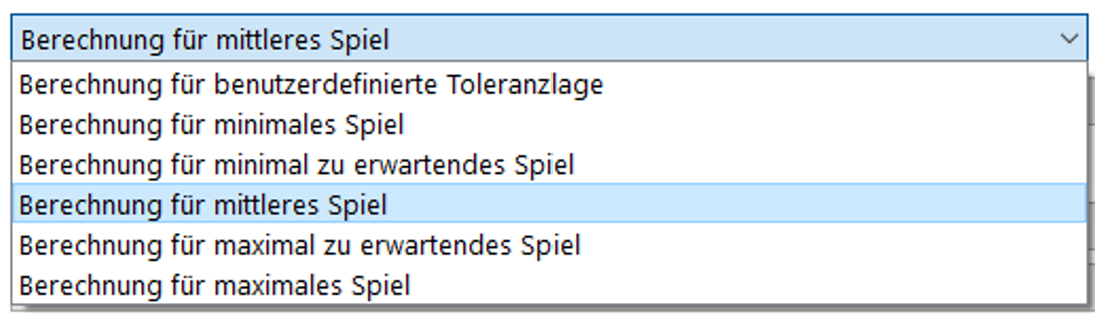
Bild 12
Der Auszug des Toleranzreports (Tabelle 2) zeigt für den kalten Montagezustand (Lastkollektiv-Element 1) die folgenden Passungsinterferenzen an B1 & B2:

Tabelle 2
4.5 Parametrierung des Vorspannweges
4.5.1 Parameter
Die Parametrierung des Vorspannweges ist aufgrund der zu untersuchenden Mindestbelastung im kritischen Lastkollektiv-Elementes 3 auszuführen.
Der Parameter B2-Pa_Li eignet sich für die Darstellung der Variierung des Vorspannweges mit seiner Definition von Axialspiel zwischen Spacer und Innenring B2 (Bild 10). In 20 Schritten soll die Rücknahme des Spacers eine Generierung von Axial-Luft zwischen Spacer und Lager-Innenring B2 durch Pa_Li abbilden. Die einhergehende negative Interferenz zwischen Innenring und Wellenmutter Pa_Ri (Bild 10) soll gleichzeitig eine nach links erwirkte Verschiebung des Innenrings um die parametrierten Werte abbilden.
4.5.2 Gemittelte Betrachtung
Es kann davon ausgegangen werden, dass die Erhöhung der Vorspannung, auch eine Erhöhung der Wellen-, Spacer- und Wellenmutter-Temperatur mit sich bringt (Bild 13):
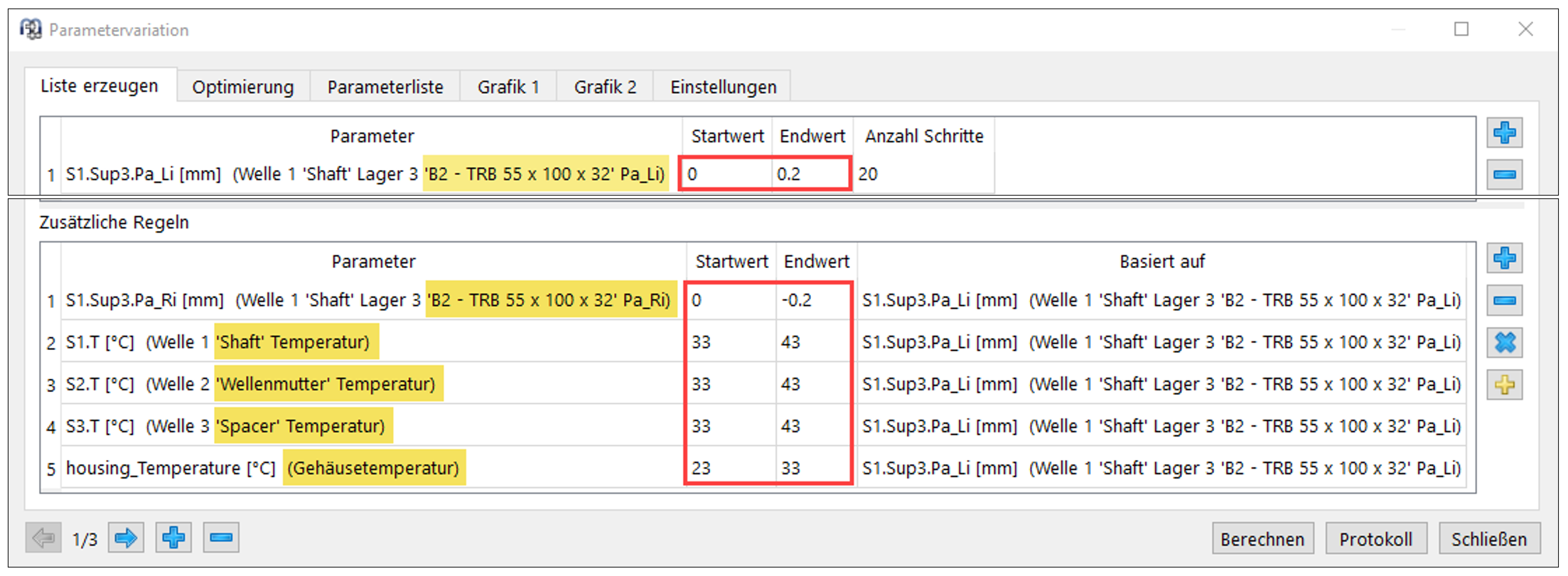
Bild 13
In der Praxis sind die hier angenommenen Temperaturen oft lediglich hypothetischen bis empirischen Charakters, da entsprechende Messungen technisch oder finanziell meist als herausfordernd zu bezeichnen sind.
Die Parametrierung unter Passungs-Übermassen entsprechend dem ‚Mittelwert‘, also ‚Berechnung für mittleres Spiel‘ an beiden Lagern (Bild 12), ergibt für Kontaktspannungen und Modifizierter Referenzlebensdauer unter Lastkollektiv-Element 3 folgende Kurven (Bild 14):
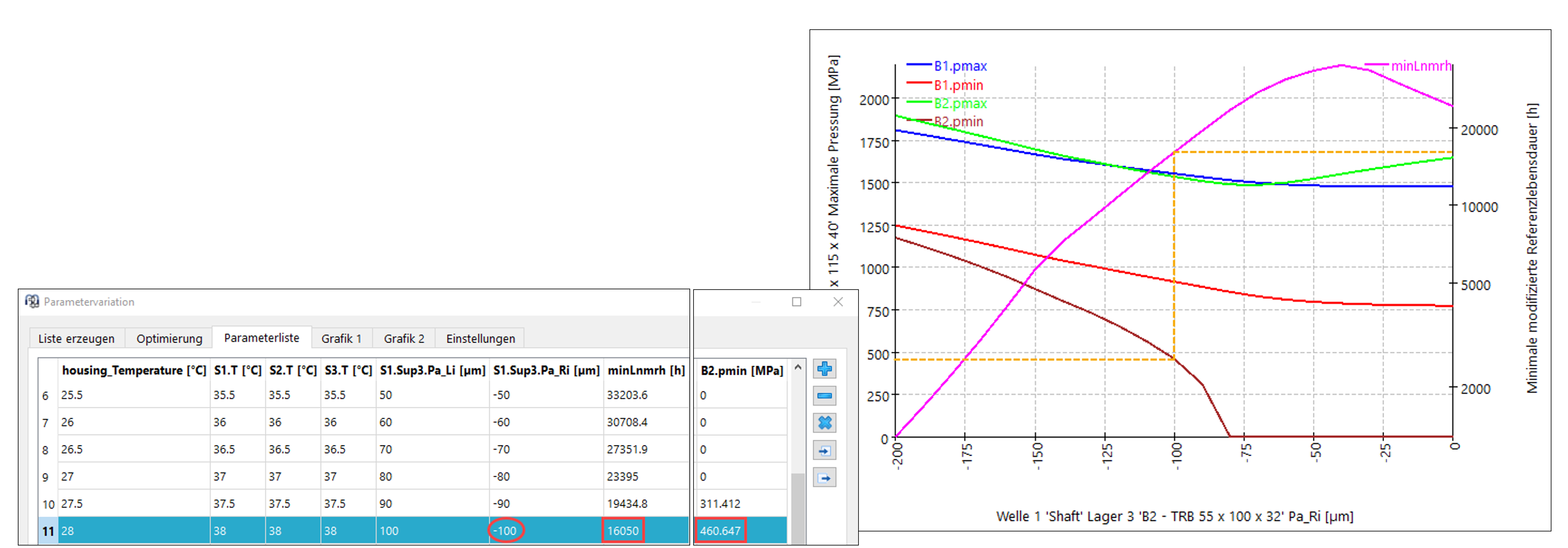
Bild 14
Ein Vorspannweg von 100 µm scheint für den kritischen Zustand von B2.pmin mit rund 460 MPa, pmin > 0 und einer entsprechenden Lebensdauer über dem geforderten Wert ein praktikabler Zustand darzustellen, wie aus der oben gezeigten Parameterliste zu entnehmen ist:
Mit der resultierenden modifizierten Referenzlebensdauer wären die ersten beiden Vorgaben aus der Zieldefinition erfüllt. Vorstehende Betrachtung mag für einen Einzelfall, unter Kenntnis der spezifischen Toleranzlagen aus Passung sowie einer Approximation des Temperaturgefälles das richtige Vorgehen darstellen. Für eine Serienproduktion bedarf es weiterer rechnerischer Unterstützung, um auch zufällige Kombinationen von inneren und äusseren Passungsinterferenzen schnell bewerten zu können. Folgender Absatz soll mittels Verwendung von spezifischer Parameterstudie in MESYS, hierzu einen Lösungsweg aufzeigen.
4.5.3. Betrachtung unter Toleranzlagen
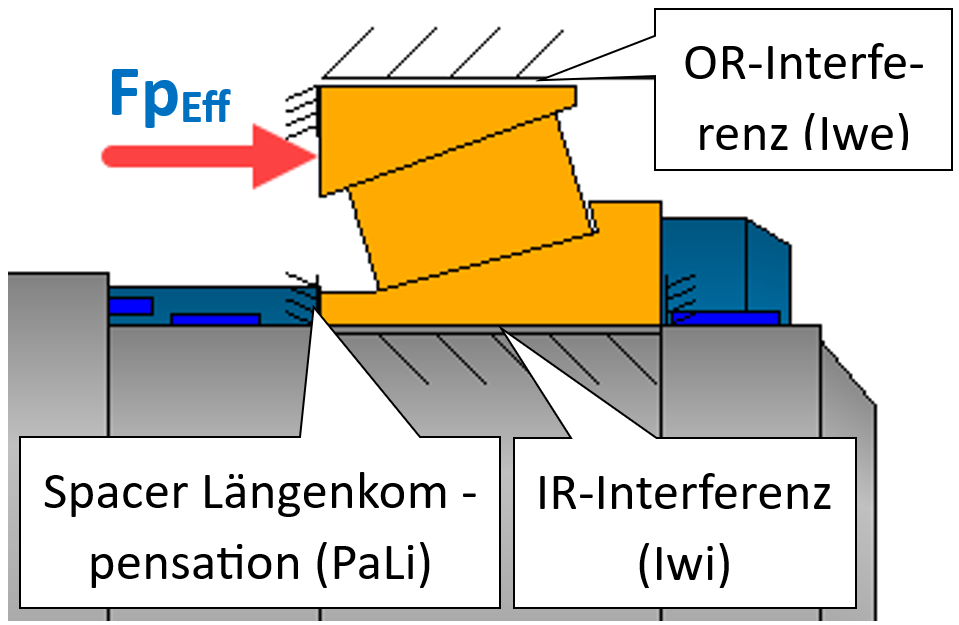
Bild 15
Die Lagervorspannkraft (FpEff) ist der dominierende Anteil an der aufzubringenden Gesamt-Spannkraft des Lagerpaares. Ist es möglich, für jede Kombination der Passungsüberdeckungen beider Lager eine geeignete, kompensierende Spacer-Länge zu bestimmen, kann davon ausgegangen werden, dass die effektive Lagervorspannkraft (FpEff) konstant bleibt. Ein derartiger Lösungsansatz kann mittels Optimierungsfunktion der Parametervariation gefunden werden und stellt damit für eine Serienproduktion ein interessantes Hilfsmittel dar.
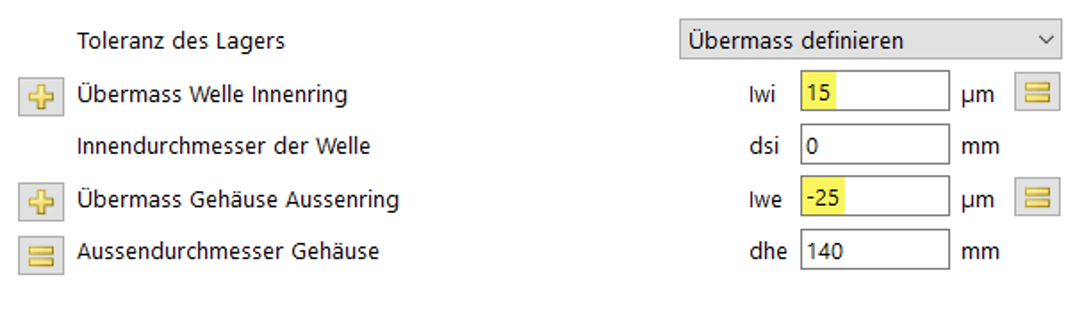
Bild 16
Ein Referenzfall (Bild 16) soll mit entsprechender Spacer-Länge in der Mitte der möglichen Toleranzlagen an beiden Lagern, ein Anhaltspunkt für die jeweilig notwendige Längenanpassung des Spacers darstellen.
Eine praktikable Einteilung für Startwert, Endwert der Passungsübermasse soll der Übersichtlichkeit der Resultate zugutekommen (Bild 17).

Bild 17
Optimierung:
MESYS ermöglicht unter Parametervariation auch die Optimierungsoption ‚Eingabe mit Nebenbedingungen minimieren‘. Damit lässt sich eine Eingabe zur Variation unter zusätzlichen Regeln und Bedingungen minimieren. Die Funktion eignet sich dazu die Delta Spacer-Länge PaLi und PaRi zu minimieren (Bild 18).
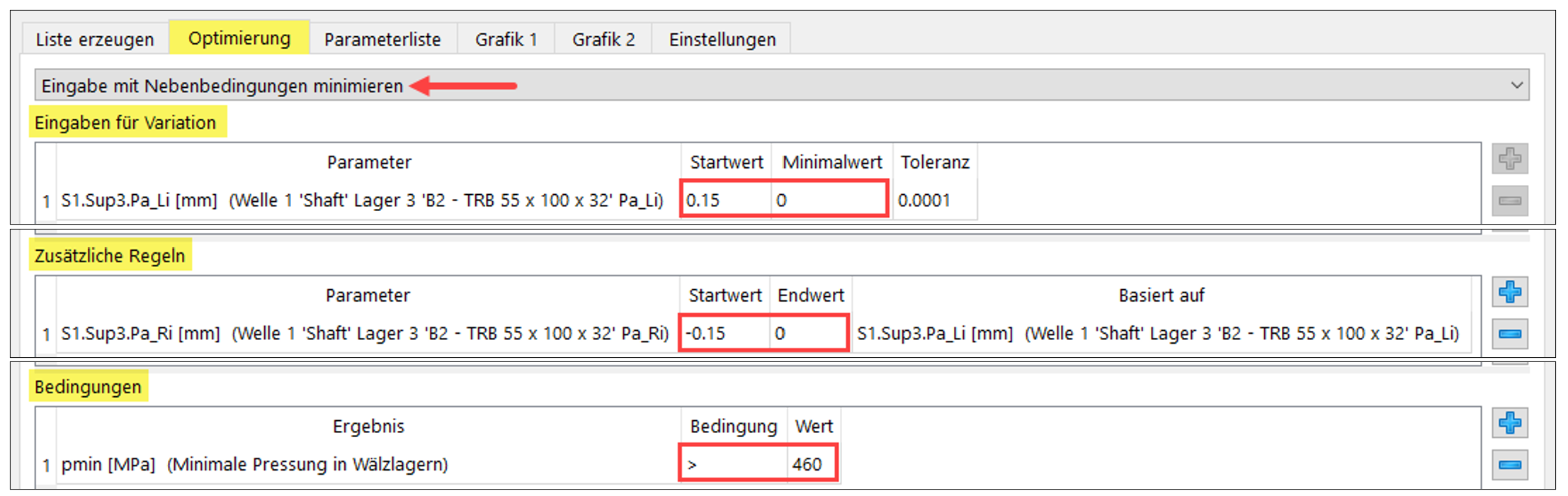
Bild 18
Die Parametrierung ist je Lager B1 und B2 unter Einbezug des Lastkollektives durchzuführen.
Exportieren
Über den Exportbefehl (Bild 19), können die Parameterlisten B1 und B2 nun in Excel weiterverarbeitet werden (Bild 20).
Bild 19
Die inkrementelle Darstellung kann hier in eine Matrix-Darstellung transponiert werden (Bild 20), um in einem weiteren Schritt dann für die praktische Verwendung, approximativ in gerundete Werte zu überführen:
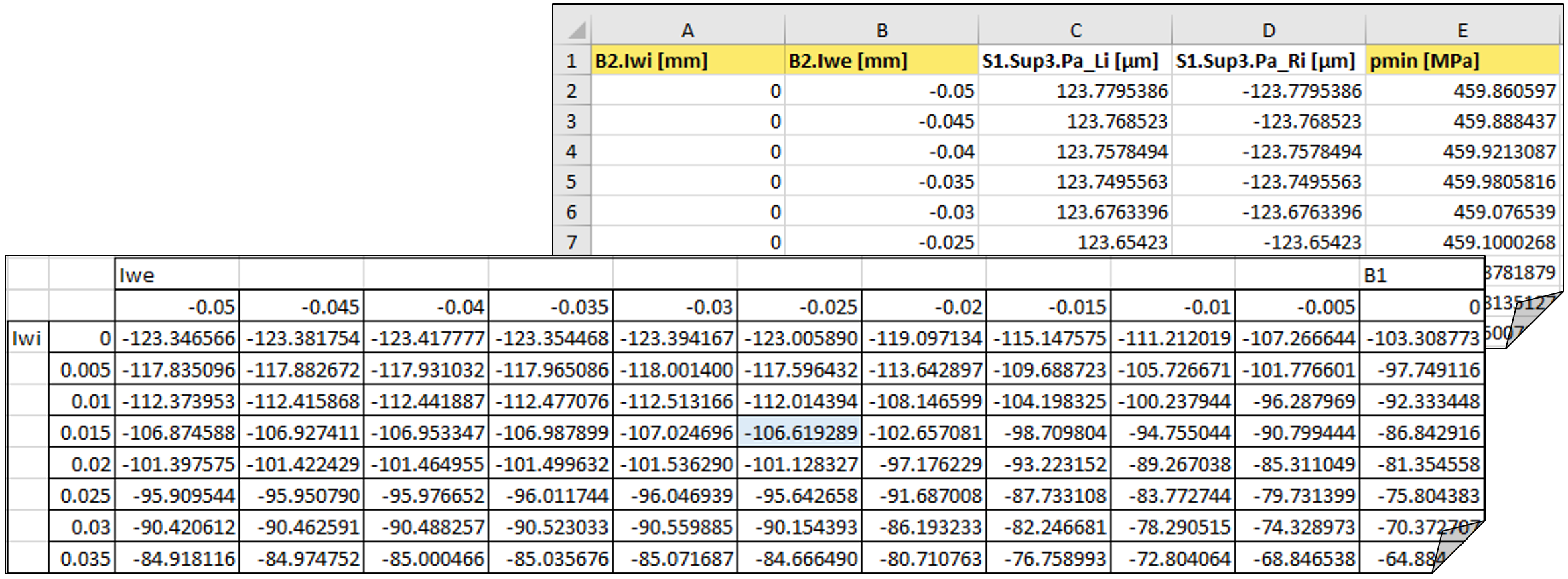
Bild 20
Damit lässt sich für beide Kegelrollenlager ein praktikable Matrix erstellen, welche die Abweichungen vom Nennmass des Spacers in Funktion der Wellensegment- und Lagerring-Istmasse tabellarisch ausgibt (Tabelle 3):
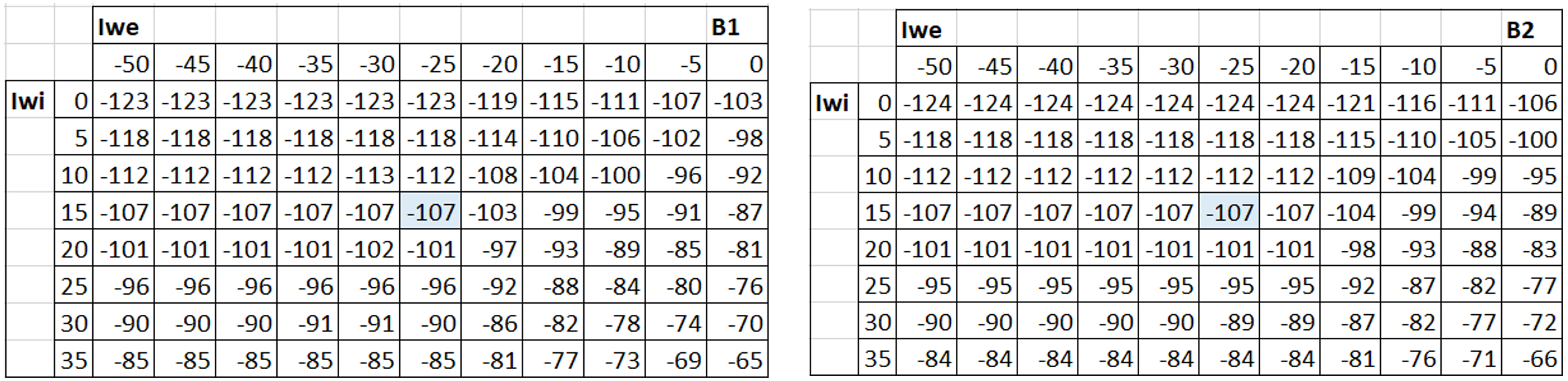
Tabelle 3
4.5.4 Berechnung des Spacers
Die Spacer-Länge kann nun über die jeweiligen Abweichungen zu dem Referenzfall approximativ bestimmt werden, wie in der Folge gezeigt wird.
Spacer-Länge über Iteration im Referenzfall
Die Abweichung der Spacer-Länge zur Nennlänge kann unter den Referenz-Interferenzen (Bild 16) und aktiviertem Lastkollektiv mittels dieser Methode, in Anwendung einer punktuellen, von Hand ausgeführter Iteration zu pmin = 460 MPa erfolgen (Bild 21).

Bild 21
Es sei diese Grösse in der Folge mit ‚Abweichung der Spacer-Länge zur Nennlänge im Referenzfall‘ PaRiRef genannt.
Spacer-Länge über Mittelwert im Referenzfall
PaRiRef kann auch näherungsweise über den Mittelwert beider errechneten PaRi’s B1 / B2 ermittelt werden (Tabelle 3), welche über diesen Ansatz gerundet ebenfalls -107 µm ergibt.
Spacer-Länge bei Abweichung vom Referenzfall
Ausgehend von Tabelle 3, lässt sich einfachheitshalber auch eine eher fertigungsorientierte Matrix erstellen, welche lediglich noch die ‚Abweichung zu PaRiRef‚ zeigt. Sei nun Letztere mit delta_PaRiRef und PaRi der Toleranzlage mit PaRiTol bezeichnet, wird der Platzhalter der Matrix für PaRiRef von -107 damit kompensiert (Tabelle 4). Ist nämlich PaRiTol im spezifischen Toleranzfeld-Fall ≙ PaRiRef, so wird delta_PaRiRef = 0:
ΔPaRiRef = PaRiTol – PaRiRef
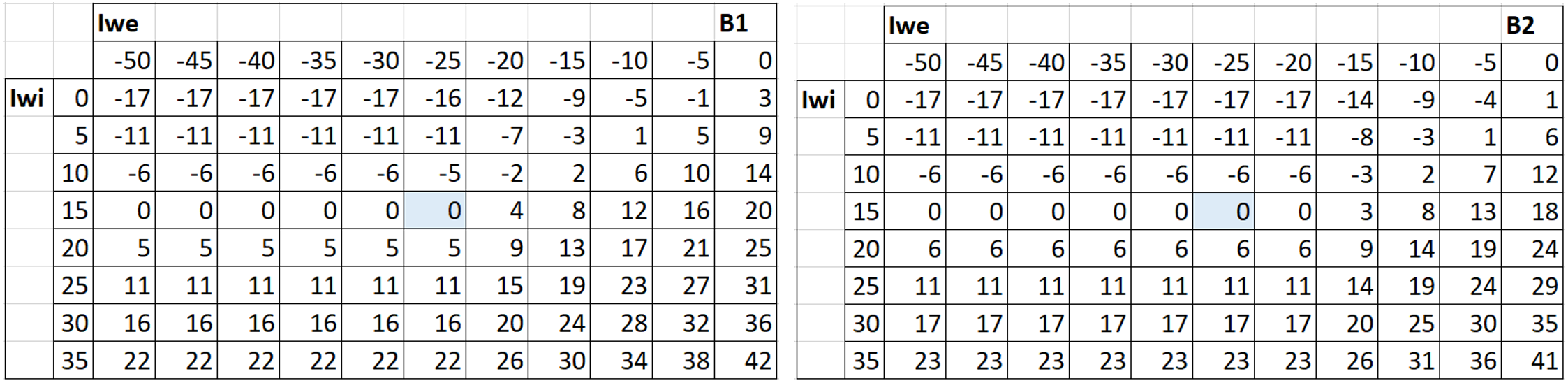
Tabelle 4
Bestimmung der Soll-Spacerlänge
Sei nun die Referenz-Spacerlänge mit RSL, die Soll-Spacerlänge mit TSL, Spacer Nennlänge mit NSL bezeichnet, so bestehen folgende Beziehungen:
RSL = NSL + PaRiRef = 20 + (-0.107) = 19.893 mm
TSL = RSL + B1.ΔPaRiRef + B2.ΔPaRiRef
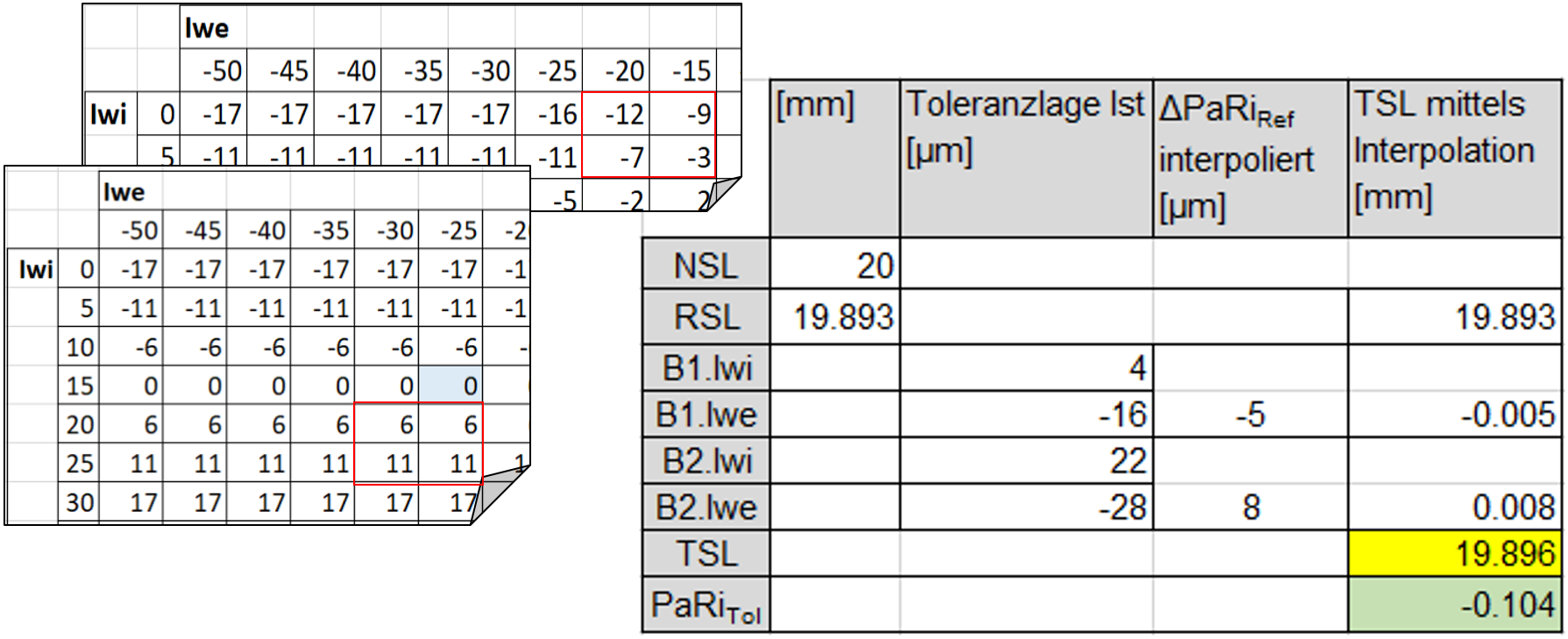
Tabelle 5
Beispiel rechts zeigt die praktische Ermittlung der Spacer-Kürzung unter Zuhilfenahme der vereinfachten Matrix aus Tabelle 4 und der Verwendung von Bilinearer Interpolation. (Tabelle 5):
Die Ausführung der Berechnung unter Eingabe der Toleranzlagen und Spacerrücknahme des vorstehenden Beispiels zeigt, dass die Bedingung der Mindestbelastung mit Ziel 460 MPa eingehalten wird (Bild 22).

Bild 22
4.6 Wellenmutter-Spannkraft
4.6.1 Allgemein
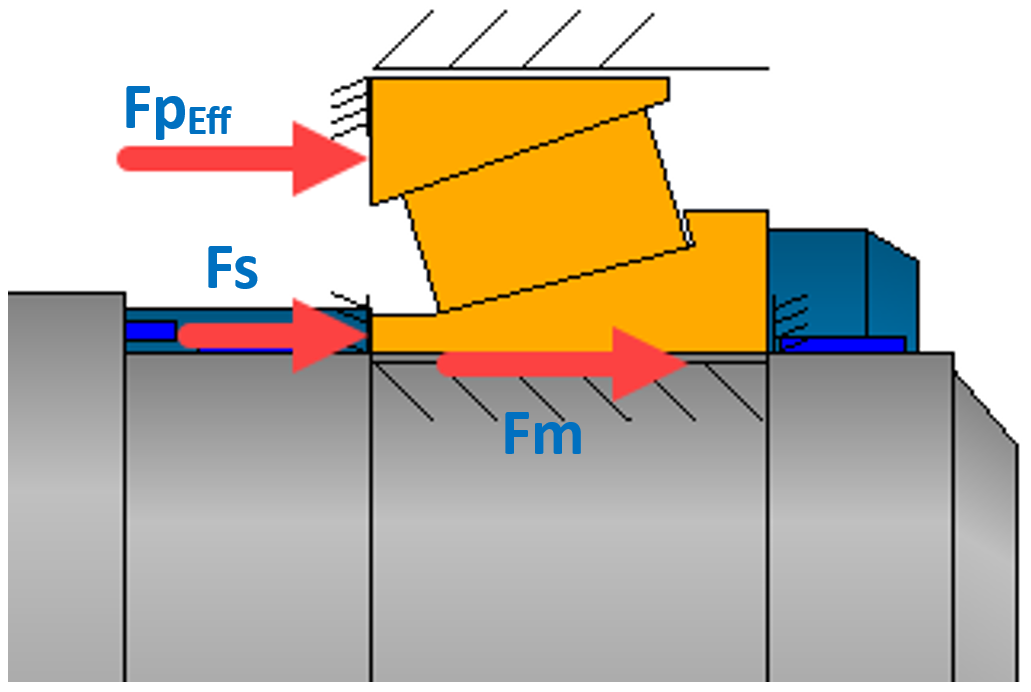
Bild 23
Die Ermittlung der notwendigen Wellenmutter-Spannkraft hat sinnvollerweise im Montagezustand, resp. im Lastkollektiv-Element 1 zu erfolgen. Die Wellenmutter Spannkraft wird üblicherweise im Zuge der rechnerischen Drehmoment-Ermittlung für die Wellenmutter erstellt. Das hier verfolgte Näherungsverfahren fasst Montagekraft (kalt), Lagervorspannkraft und zusätzliche Festhaltekraft zur erforderlichen Gesamt-Spannkraft zusammen (Bild 23).
- Montagekraft Fm
- Lagerpaar-Vorspannkraft FpEff
- Zusätzliche Festhaltekraft Fs
4.6.2. Montagekraft
Die Montagekraft (Fm) ist bei korrekter Montageprozedur lediglich innen zu quantifizieren (Ffit_i; Tabelle 6). Sind Wälzlager ohne Temperaturgefälle zu montieren, kann die Montagekraft weggelassen werden.
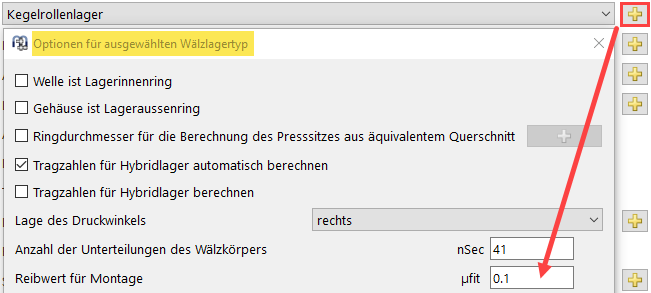
Bild 24
Reibwert
Sofern unter Lager-Option ein Reibwert für Montage definiert ist (Bild 24), wird im Toleranz-Protokoll auch eine axiale Montagekraft angezeigt.
Spezifische Montagekraft
Mittels des Toleranzreports zu Lager B2 kann die Montagekraft unmittelbar angezeigt werden (Tabelle 6).
Die Montagekraft (Fm) kann hier unter Minimum bis Maximum ausgelesen werden und bezieht sich unter Berücksichtigung von elastischer Aufweitung der Ringe auf die gewählten Passungstoleranzen. Die Werte in Tabelle 6 entsprechen B2 im Lastkollektiv-Element 1 unter dem iterierten Referenzfall (Bild 21).

Tabelle 6
Montagekraft über Toleranzlagen
Die Information zur Montagekraft aus dem Toleranzreport reicht für eine industrielle Fertigung als Grundlage nicht. MESYS bietet hierzu die Möglichkeit, Montagekräfte über Kombination von Toleranzlagen mittel Parametervariation zu ermitteln.
Das Exportfile der Parameterliste aus der Berechnung der Spacer-Rücknahme für Lager B2 (Bild 19) ermöglicht nun die Ermittlung der Montagekraft über alle im Bereich möglichen Kombinationen an Passungs-Toleranzlagen. Die jeweilige Wirkung aus Axialkraft des verspannten Lagerpaars kann als angeglichener Wert betrachtet werden, welcher auf die Anpassung des Spacers zurückzuführen ist.
Parameter wie Montagekraft B2.Ffit oder die Spannung an der Wellenmutter S2.Sup1.Fx können bei diesem Schritt zusätzlich in die Liste geladen werden (Bild 25).
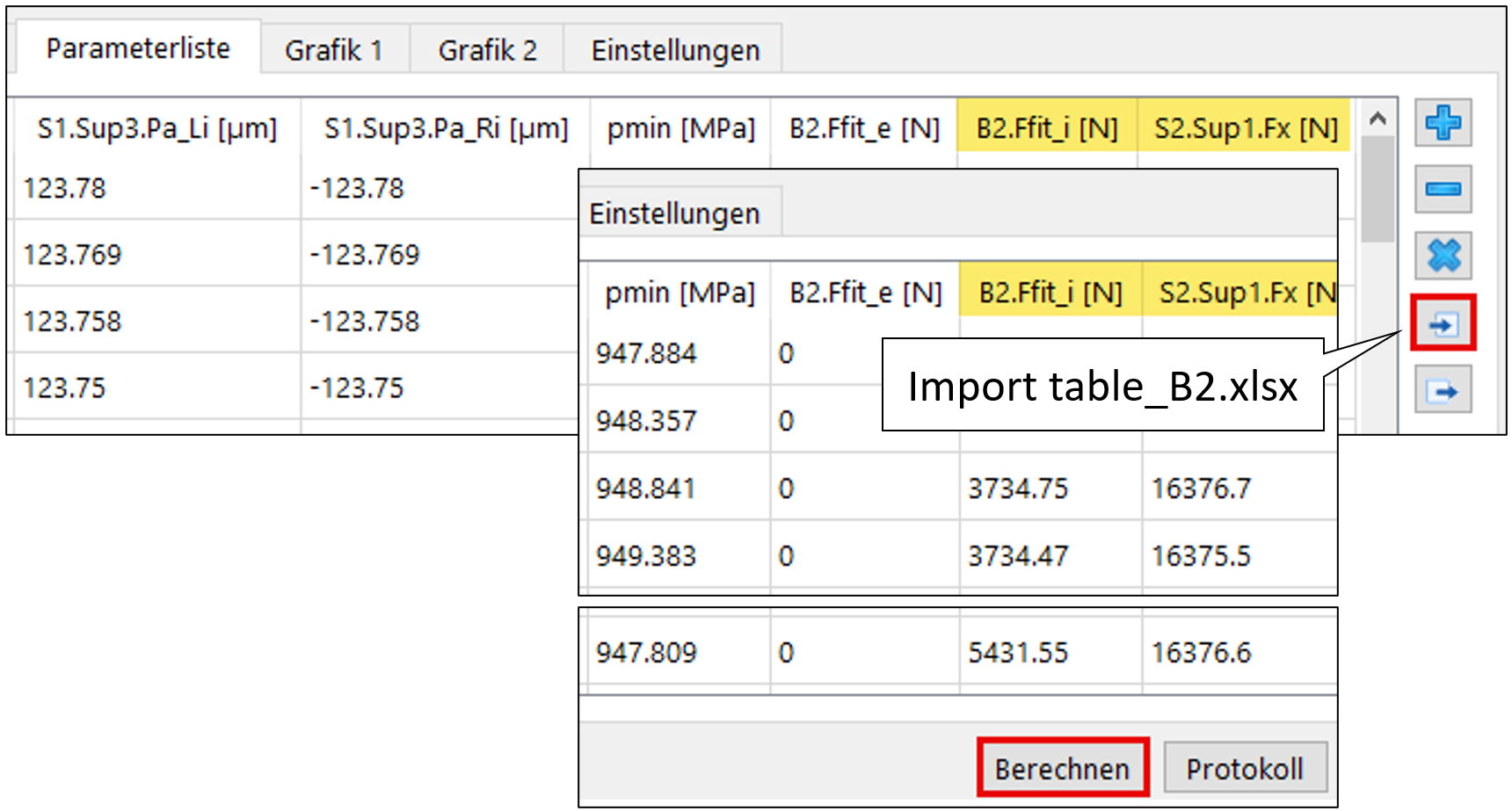
Bild 25
Das unter vorgewähltem Lastkollektiv-Element 1 (Montage) importierte File erzeugt nun nach aktivieren des Berechnungsschrittes nebst den inneren und äusseren Montagekräften für B2 (Ffit) auch die Spannkraft des Lagerpaares an der Wellenmutter S2.Sup1.Fx (Bild 25).
Damit ist die Abhängigkeit der Montagekraft an Lager B2 von den Passungsinterferenzen und den Wirkungen der elastischen Ringaufweitung mit adäquater Approximation wiedergegeben.
4.6.3 Zusätzliche Festhaltekraft
Eine zusätzliche Festhaltekraft (Fs) für den verspannten Block wird in der Praxis präventiv für eine zusätzliche Steifigkeit zur Kompensation von dynamischen Krafteinleitungen angewendet. Hierbei kann für den Kontaktspannungs-Wert (MPa) an der Interferenz zum Spacer eine Grösse basierend auf Wälzlager-Herstellerangaben oder über empirische Herangehensweise gewählt werden.
Fs als Summand an die Mutter-Spannkraft, ist hier mit 8’000 N bewertet.
4.6.4 Summe Spannkraft
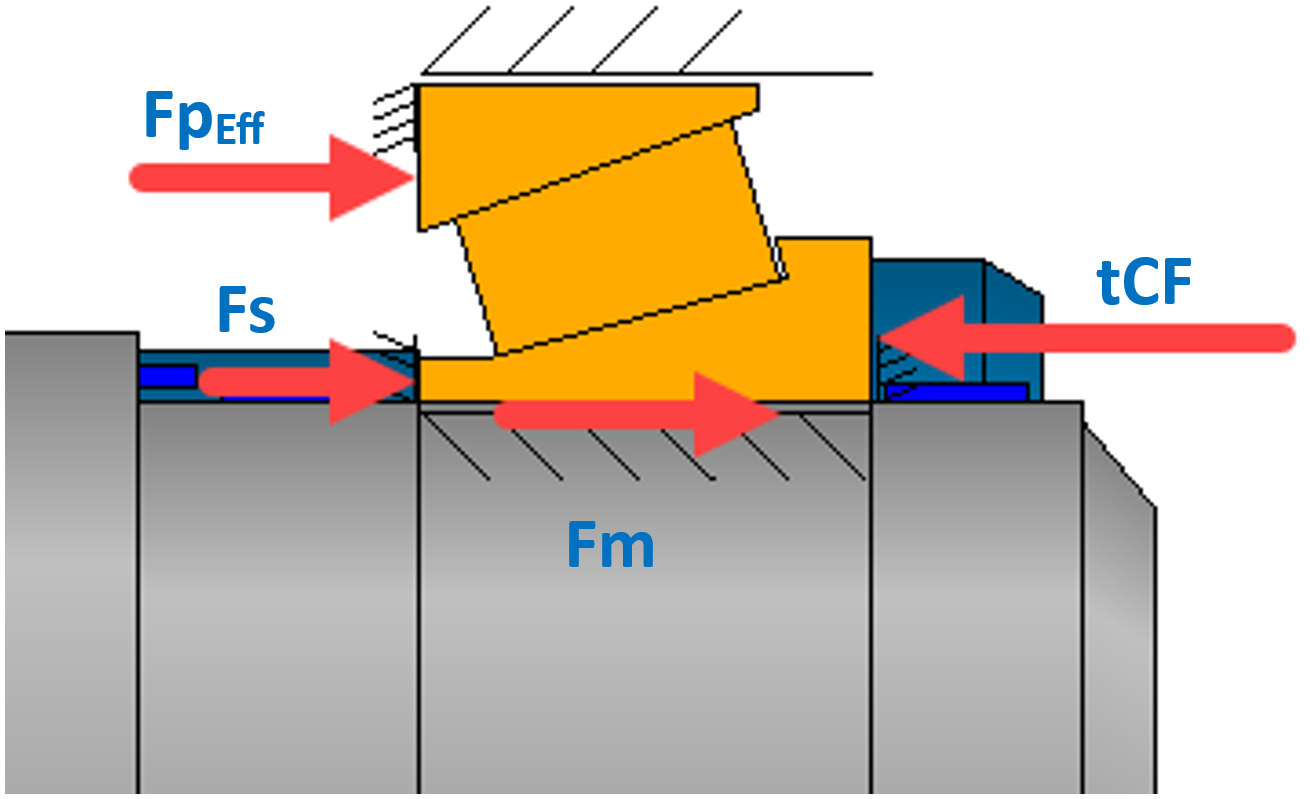
Bild 26
Die Summe der anvisierten Mutter-Spannkraft (tCF) (Bild 26) aus effektiver Vorspannkraft des Lagerpaares + Montagekraft + zusätzlicher Festhaltekraft stellt sich gemäss vorstehender Definition nun wie folgt dar:
tCF = Fm+ FpEff + Fs
Durch die Ergänzung eines festen Wertes für Fs gemäss 4.6.3 in ein Exportfile (Bild 27), ergibt sich nun ein praktikables Werkzeug zur schnellen Bestimmung einer zur spezifischen Spacer-Länge gehörende Wellenmutter-Spannkraft.
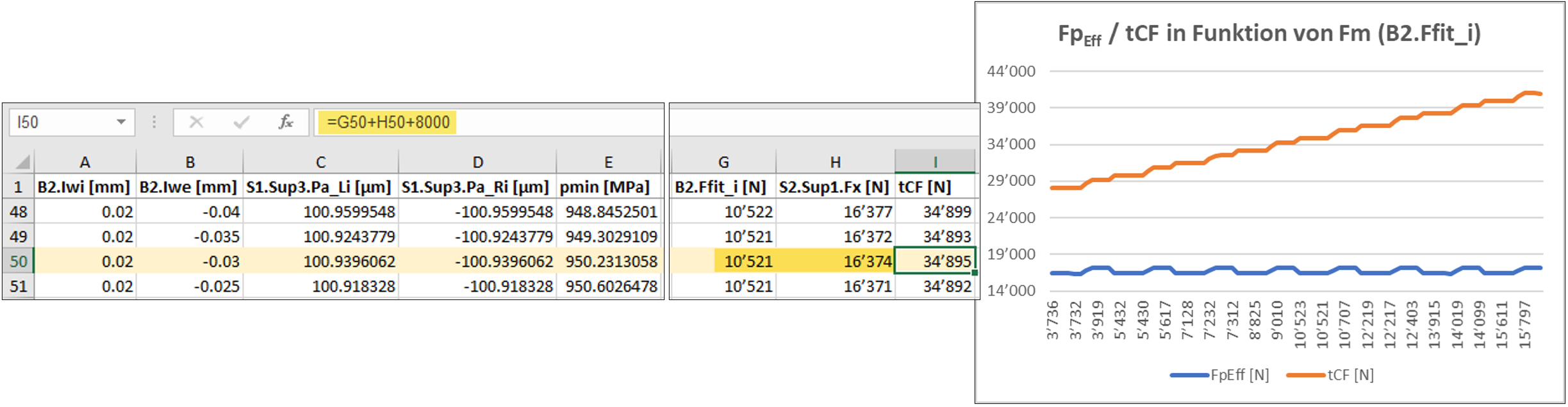
Bild 27
Die Grafik in Bild 27 zeigt die unter Einfluss der Spacer-Anpassung quasi konstante Lagervorspannung FpEff (S2.Sup.Fx) über innere Montagekraft (B2.Ffit_i). Dieser Effekt verändert sich auch nicht unter Abweichung von der Referenz-Toleranzlage bei Lager B1. Die in 4.5.4 beschriebene Herangehensweise berücksichtigt ja eine entsprechende Spacer-Anpassung unter dem Effekt beider Lagersitze. Insofern kann in qualitativer Approximation, eine Ableitung der notwendigen Spannkraft der Wellenmutter in Funktion der Variation der Toleranzlage des vorzuspannenden Lagers B2, sowie einer Rundung bzw. Interpolation der in 4.6.2 importierten Parameterliste als angemessener Ansatz gelten.
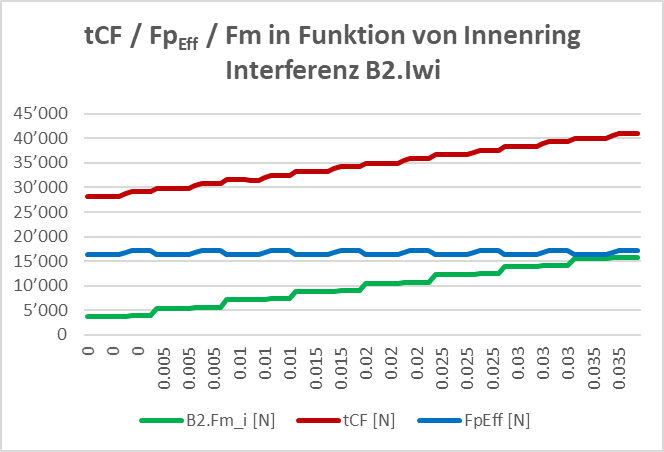
Bild 28
Die Summanden der Wellenmutter-Spannkraft Fm + FpEff + Fs können durchaus einzeln gerundet oder interpoliert werden. Aufgrund der Spacer-Anpassung über alle Toleranzlagen – auch an der äusseren Interferenz, bleibt die Lager-Vorspannkraft FpEff quasi-konstant (Bild 28). Die Funktion der Variation der notwendigen Gesamt-Wellenmutter-Spannkraft tCF darf daher in der Montagekraft am Innerring gesucht werden. Daraus folgt, dass die äussere Toleranzlage und deren Interferenz (Iwe) hier nicht relevant und für die Praxis die eindimensionale Betrachtung durchaus zielführend ist.
Für die spezifische Toleranzlage resultiert die Montagekraft Fm mit 10’521 N und die Lagervorspannung FpEff mit 16’374 N. Daraus generiert sich eine Wellenmutter-Spannkraft tFC von 34’895 N (Bild 27).
5. Wirkung & Nachweis
5.1 Beispiel
Ausgehend von der Beispiel- Berechnung der Spacer-Länge in 4.5.4 sei eine Wellenmutter-Spannkraft zu bestimmen. Die Spacer-Kürzung (‚Rücknahme‘, Tabelle 5) wurde mit -104 µm für eine Soll-Spacer-Länge SSL von 19.896 mm bestimmt.
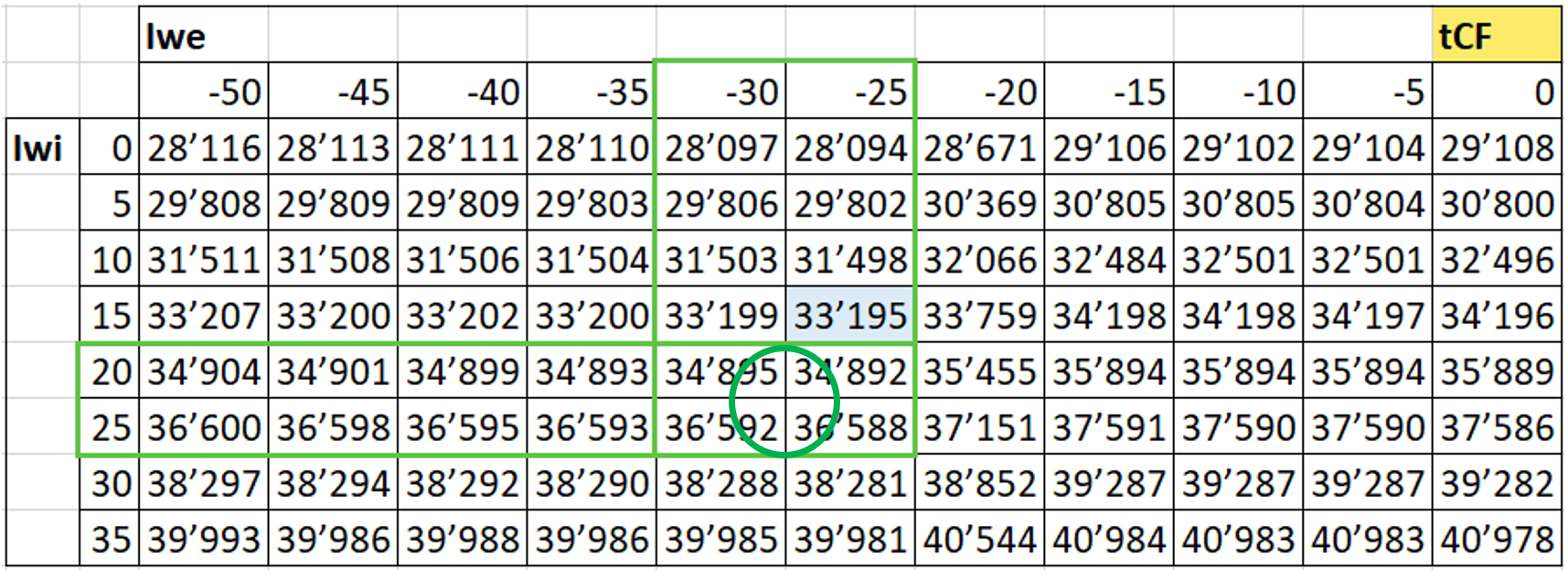
Tabelle 7
Bilineare Interpolation von tCF
Die in eine Matrix-Darstellung überführte und in 4.6.4 erzeugte Tabelle dient als Basis für die Ermittlung der Wellenmutter-Spannkraft tCF (Tabelle 7).
Der Wert für die Gesamt Spannkraft der Wellenmutter tCF beträgt aus entsprechender Interpolation 35’572 N.
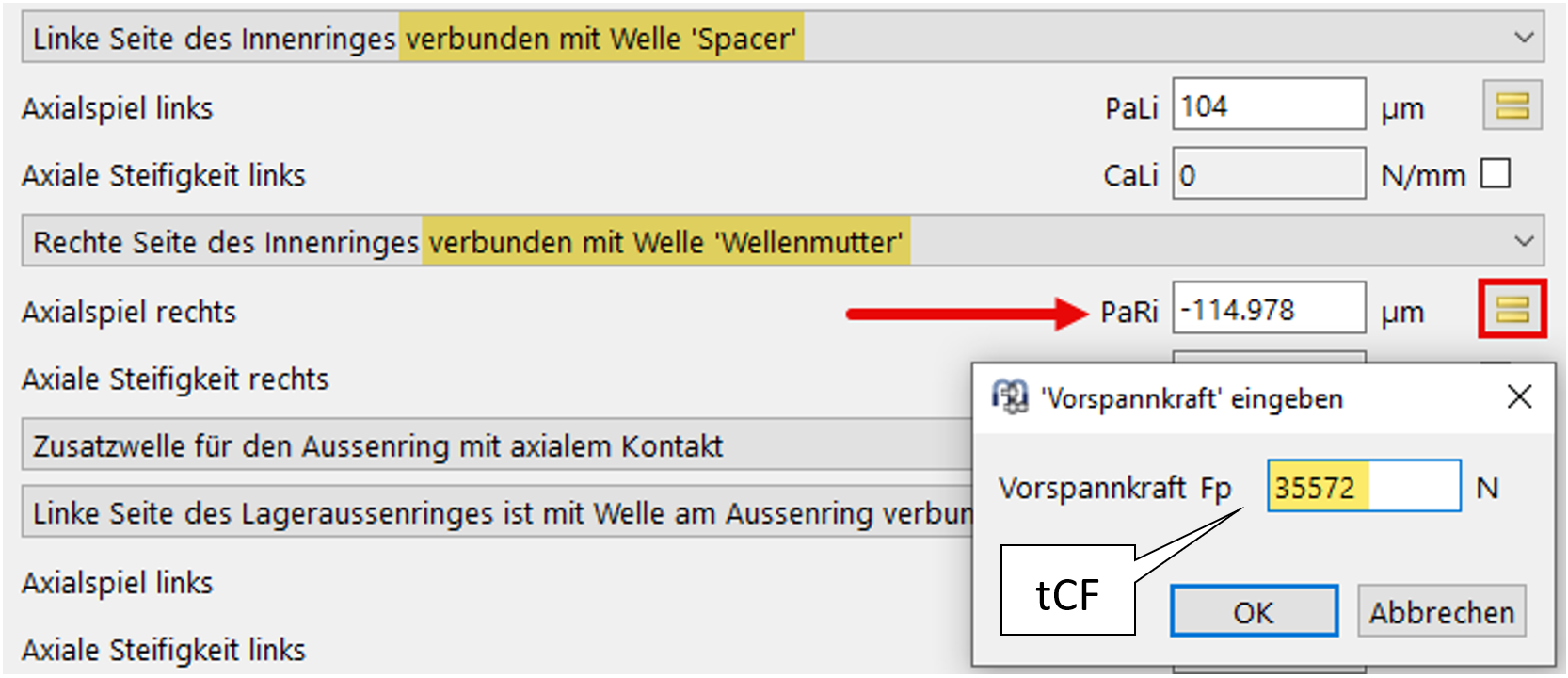
Bild 29
Da nun die Spannkraft der Wellenmutter bekannt ist, kann diese in MESYS bequem über die ‚=‘ – Schaltfläche für PaRi vorgegeben werden (Bild 29).
Hinweis: Die Spannkraft der Wellenmutter kann auch über die Randbedingung an der Wellenmutter selbst vorgegeben werden.
5.2 Resultate
Die Ausgabe der Resultate nach Eingabe der dem vorstehenden Beispiel entsprechenden Werten, zeigt im unteren Fenster der Bedieneroberfläche die erwarteten Axialkräfte, Kontaktspannung und Lebensdauer (Bild 30).
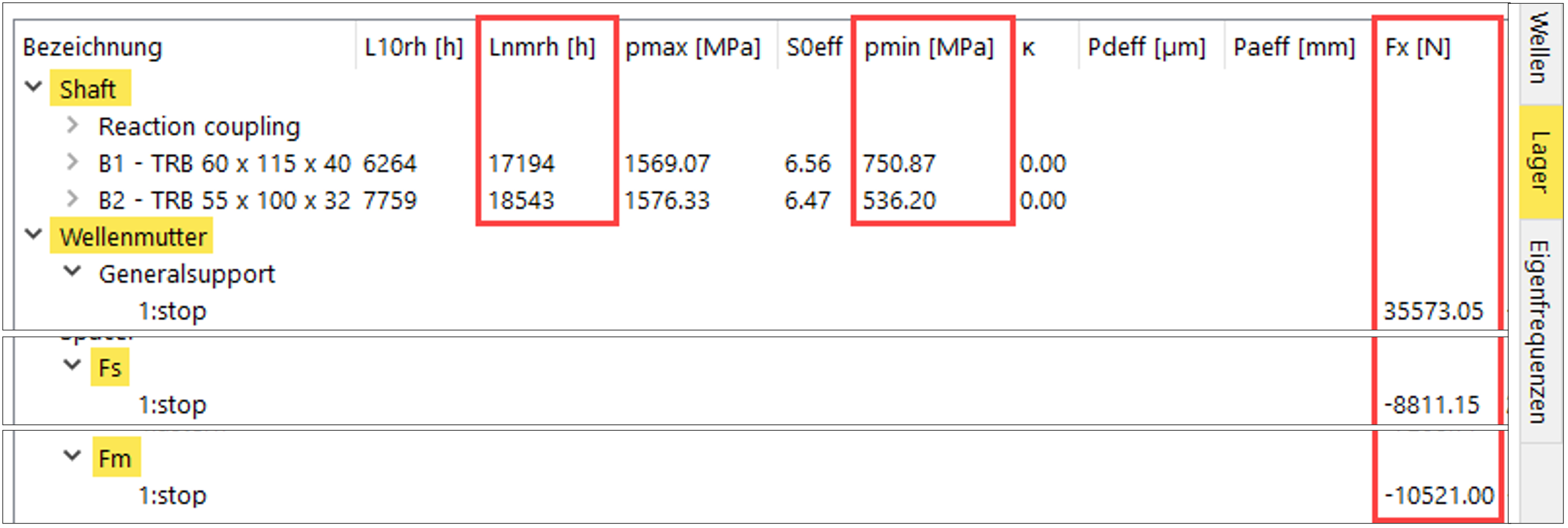
Bild 30
5.3 Nachweis
Folgendes kann mit Bezug zu den Argumenten der Zielumsetzung über das gesamte Lastkollektiv erwähnt werden:
- Die Mindest-Last ist eingehalten
- Die Mindest-Lebensdauer ist eingehalten
- Die Anstellkraft der Wellenmutter ist spezifisch ausgelegt
- Die vorstehend dargestellten Methoden der Approximation sind über Passungs-Toleranzlagen hinweg robust
5.4 Weitere Anmerkungen
Die hier beschriebene Auslegung einer Vorspannung und Anstellung eines Kegelrollenlager-Paares erhebt nicht den Anspruch der Vollständigkeit. Die Auslegung basiert auf gewissen Annahmen, die für den jeweiligen Anwendungsfall anzupassen sind. Die Steifigkeit der Lager hängt von deren Innengeometrie ab, die den Endanwendern oft nicht bekannt ist.


